Las Razones Trigonométricas de un ángulo agudo son el seno, el coseno y la tangente. Siendo la razón el cociente entre dos números. Para referirnos a ángulos, normalmente se utilizan las letras griegas como:
α alfa
β beta
γ gamma
φ fi
A continuación se muestras la razones trigonométricas del ángulo α:
Vamos a estudiar todas las posibles razones entre dos de los lados de un triángu-
lo rectángulo.
Sobre un ángulo agudo, a, construimos un triángulo rectángulo, ABC. Damos las siguientes definiciones con sus correspondientes abreviaturas:
seno de a = longitud del cateto opuesto a α longitud de la hipotenusa
coseno de a = longitud del cateto contiguo a α longitud de la hipotenusa
tangente de a = longitud del cateto opuesto a α longitud del cateto contiguo a a
Estas relaciones se llaman razones trigonométricas del ángulo a.
Cálculo de las razones trigonométricas de un ángulo
La propia definición nos proporciona un método para calcular las razones trigonométricas de un ángulo agudo:
Se dibuja el ángulo. Desde un punto, B, de uno de los lados se traza una perpendicular al otro lado. De este modo se forma un triángulo rectángulo ABC. Se miden los lados:
AC = 41 mm, BC = 28 mm, AB = 50 mm
Ahora, con estos datos, calculamos las razones trigonométricas:
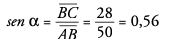
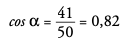
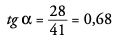
Podríamos medir el ángulo con el transportador. Obtendríamos α = 34°. Por tanto:
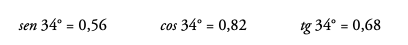
Estas medidas son aproximadas, así como las relaciones finales.
Relaciones Trigonométricas Fundamentales
Los valores de sen, cos y tg de un mismo ángulo no son independientes, sino que están relacionados, de tal modo que conociendo uno de ellos, podemos calcular los otros dos. Las relaciones que los ligan son las siguientes (se las suele llamar relaciones fundamentales):

Estas igualdades son fáciles de demostrar:
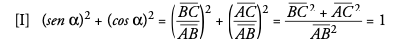
pues por el teorema de Pitágoras se cumple que:
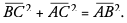
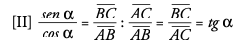
Ejercicio:

0 comentarios