Las función cuadrática es continua en todo R y se representan mediante una parábola que tiene su eje paralelo al eje Y. Es de la forma:
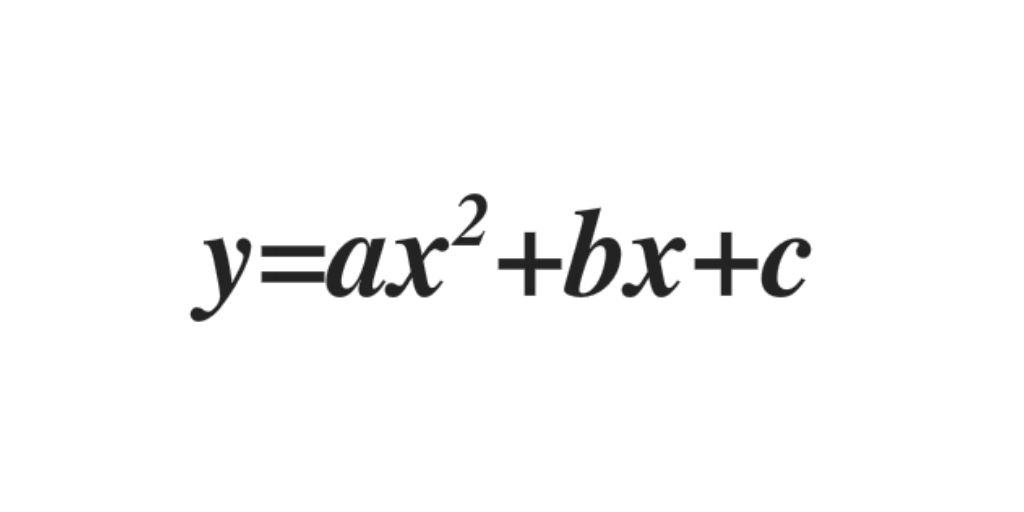
- Si a>0 tienen todas las ramas hacia arriba.
- Si a<0 tienen todas als ramas hacia abajo.
- Cuanto mayor es |a|, más estilizada es la parábola.
Para calcular el vértice de la función cuadrátia se aplica la siguiente fórmula:
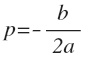
Para representar una función cuadrática seguimos los pasos:
- Hallar la el punto del vértice de la función.
- Obtener los puntos de corte con los ejes.
Se resuelve la ecuación ax2+bx+c=0 para hallar el corte con el eje X y posteriormente se obtiene el corte con el eje Y: (0,c).
- Dada la función y=x2+6x-16:
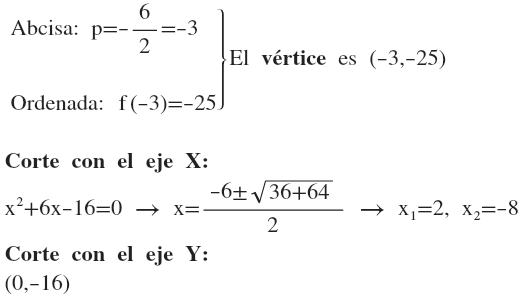
- Representación gráfica:
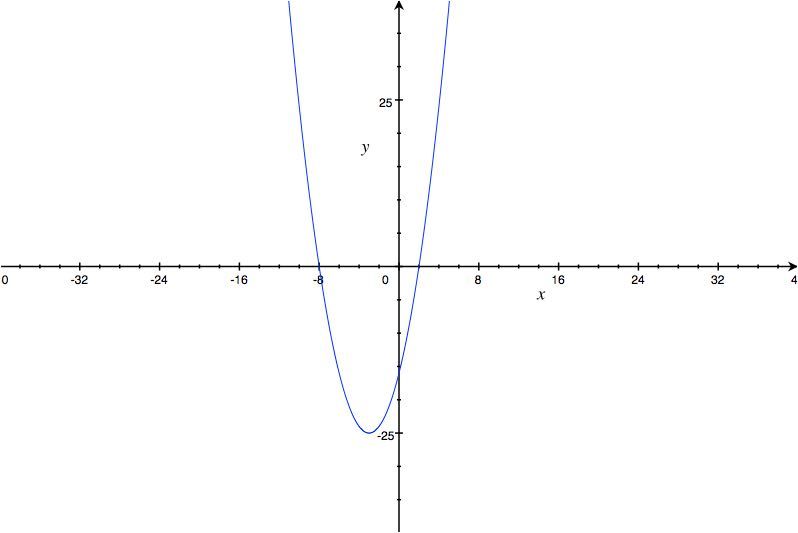

Gráfica las siguientes funciones cuadráticas hallando el vértice y los puntos de corte con los ejes de coordenadas: 2. F(x)=x² -1