Teorema de Pitágoras

Según el Teorema de Pitágoras, dado un triángulo rectángulo: la suma del cuadrado de sus catetos es igual al cuadrado de su hipotenusa. Esto solo se cumple si el triángulo es rectángulo.

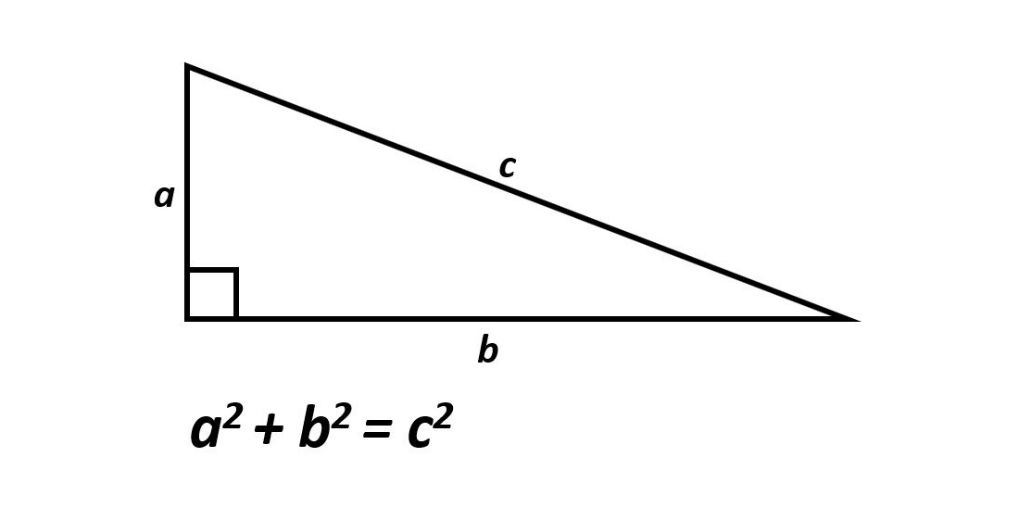
En un triángulo rectángulo, los lados menores son los que forman el ángulo recto. Se llaman catetos. El lado mayor se llama hipotenusa. b y c son los catetos. a es la hipotenusa. 
El teorema de Pitágoras dice que:
a2 =b2 +c2
Es decir, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. Y esto es verdad solamente si el triángulo es rectángulo.

Demostración del Teorema de Pitágoras

Para demostrar el teorema fíjate en las siguientes imágenes:

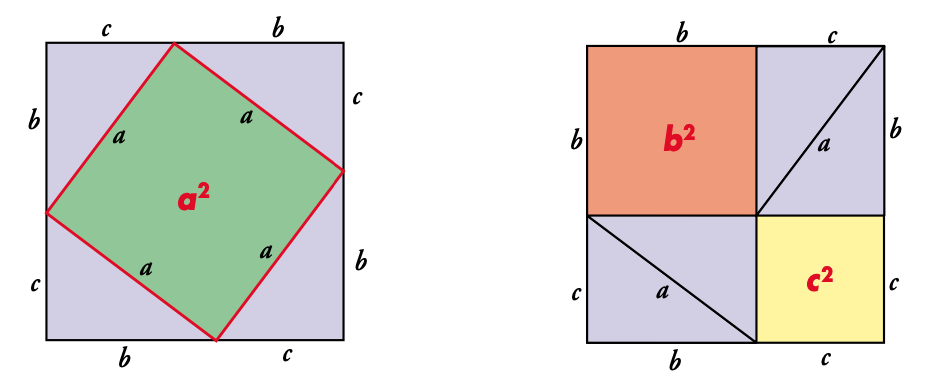
• Los dos cuadrados grandes son iguales. Su lado es c + b.
• En el primero, hay un cuadrado de área a² y cuatro triángulos.En el segundo, hay dos cuadrados de áreas c² y b² y cuatro triángulos.
• En el segundo, hay dos cuadrados de áreas c² y b² y cuatro triángulos.
• Por tanto, al suprimir los cuatro triángulos de cada uno, las áreas de lo que que- da coinciden: b² + c² = a².

¿Cómo saber si un Triángulo es Rectángulo?

a, b, c son los lados de un triángulo, y a es el mayor.
A continuación veremos cómo distinguir distintos tipos de triángulos según el Teorema de Pitágoras.

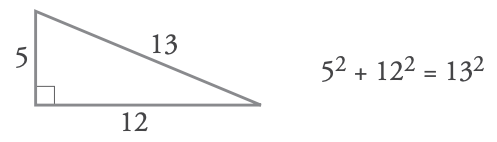
• Si b² + c² = a², el triángulo es rectángulo.
  
• Si b² + c² < a², el triángulo es obtusángulo.
  
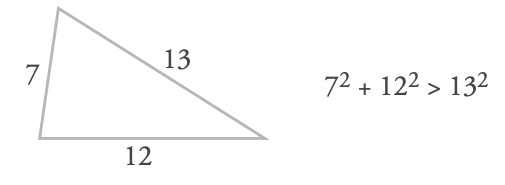
• Si b² + c² > a², el triángulo es acutángulo.
  

Aplicación del Teorema de Pitágoras

Conociendo los dos catetos, calcular la hipotenusa
Si de un triángulo rectángulo conocemos los dos catetos, podemos calcular la hipotenusa:

Conociendo la hipotenusa y un cateto, calcular el otro
Si de un triángulo rectángulo conocemos la hipotenusa y un cateto, podemos calcular el otro cateto:

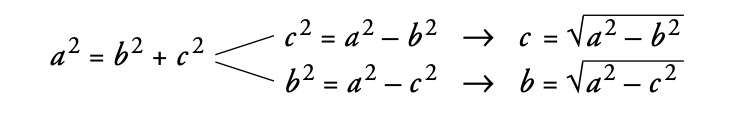
Ejercicios

1. Responde redondeando el resultado a dos decimales:

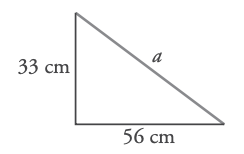
2. Calcula la hipotenusa: