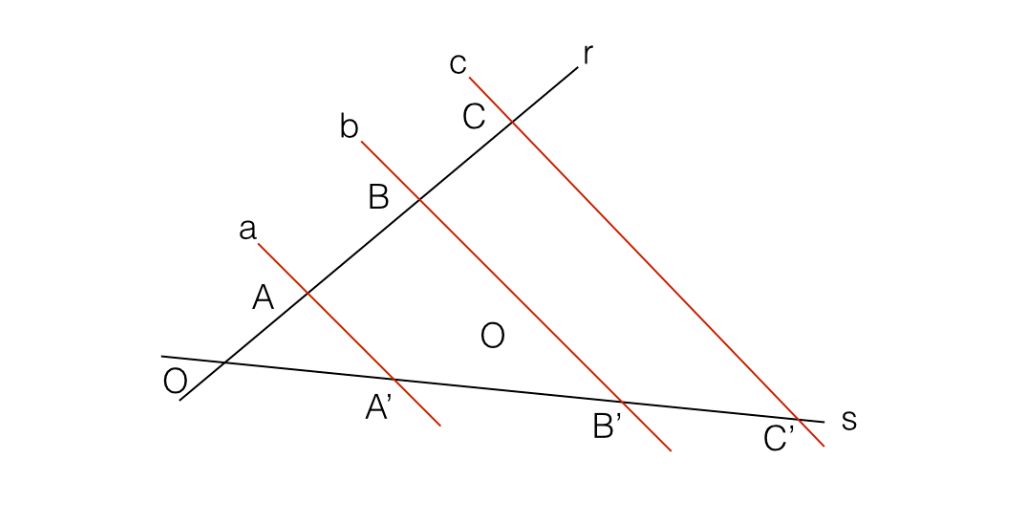
Según el Teorema de Tales podemos afirmar que si se traza una línea paralela a cualquiera de los lados de un triángulo, obtendremos un triángulo semejante al triángulo original como resultado. Esto quiere decir que si cortamos un triángulo mediante una recta, siendo esta paralela a uno de sus lados, el triángulo resultante será semejante al original. Si las rectas a, b y c son paralelas y cortan a otras dos rectas r y s, entonces diremos que los segmentos que resultan en ellas, son proporcionales.

También ocurre lo recíproco: si los segmentos AB y BC son proporcionales a A’B’ y B’C y las rectas a y b son paralelas, entonces la recta c es paralela a ellas.El teorema de Tales sirve para estudiar la semejanza de triángulos
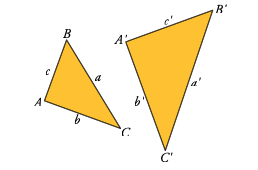
Triángulos Semejantes:
Dos triángulos semejantes tienen sus lados proporcionales y sus ángulos respectivamente iguales:
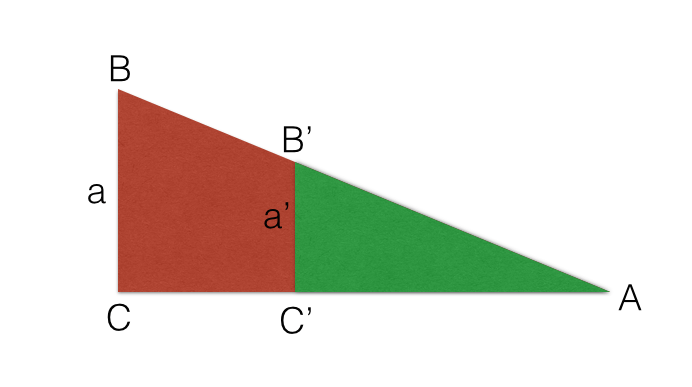
Ejemplos de Teorema de Tales
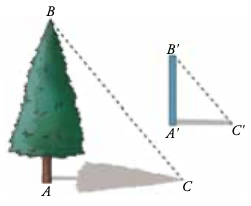
Los triángulos ABC y AB’C’ tienen un ángulo en común, el A. Es decir, el pequeño triángulo está encajado en el grande.
Además, los lados opuestos a A son paralelos. Decimos que esos dos triángulos están en posición de Tales. Dos triángulos en posición de Tales cumplen la razón de Semejanza.
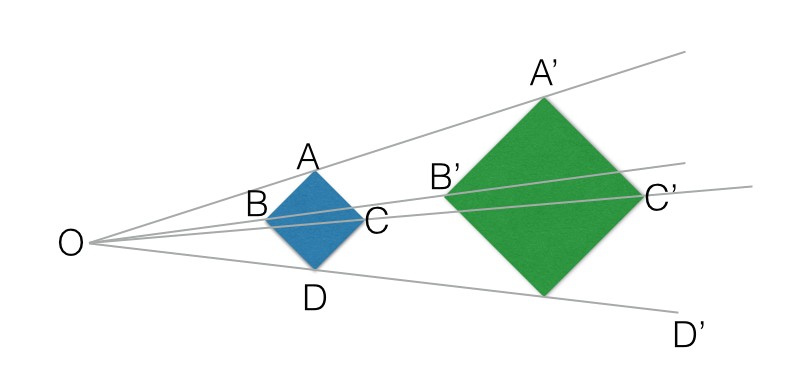
Homotecia
Se llama homotecia de centro O y razón k a una transformación que hace corresponder a cada punto P otro P’ tal que:
Ejercicios de Teorema de Tales
Ejercicio 1:
Ejercicios del Teorema de Tales
Ejercicio 2:


0 comentarios