Un monomio es una expresión algebraica simple formada por un producto de letras y números. La parte literal son las letras y la parte numérica son los números.
- El coeficiente de un monomio es el número que multiplica la parte literal.
- El grado de un monomio es el número total de factores que forma su parte literal.
- Dos monomios son semejantes cuando tienen idéntica la parte literal.
Veamos tres ejemplos de monomios:
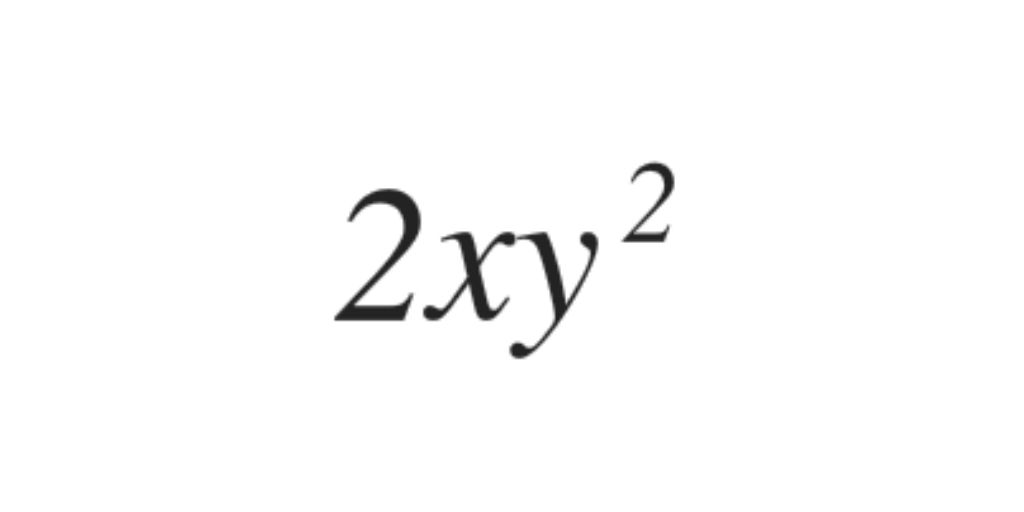
La parte literal es xy2 y su grado es 2.
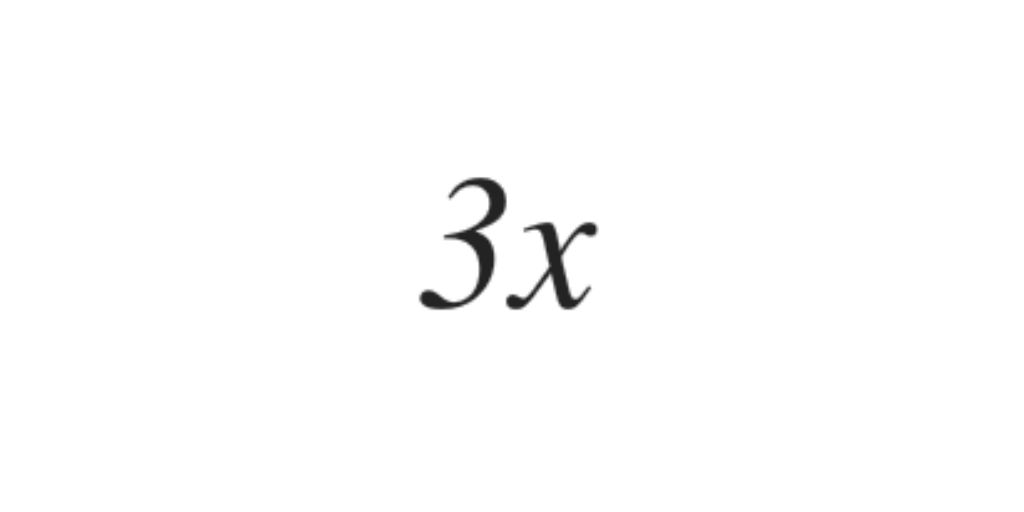
La parte literal es x y su grado es 1.
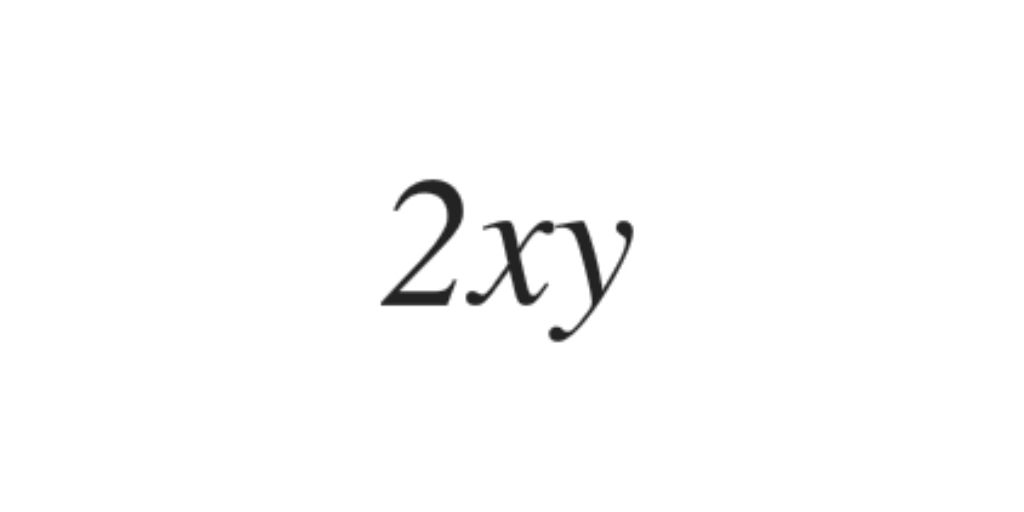
La parte literal es xy y su grado es 2.
Suma y resta
La suma y resta de monomios solo puede hacerse cuando tienen la misma parte literal, es decir, si son semejantes. Si se suman o restan no siendo semejantes se deja indicado.
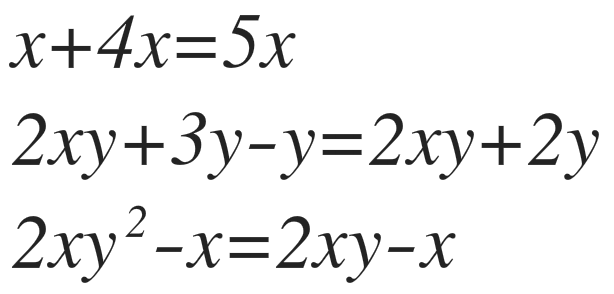
Multiplicación
Para multiplicar monomios hay que tener en cuenta que un monomio es un producto, por tanto, al multiplicarlos obtenemos otro producto con más factores, es decir, otro monomio.
El producto de dos monomios es siempre otro monomio.
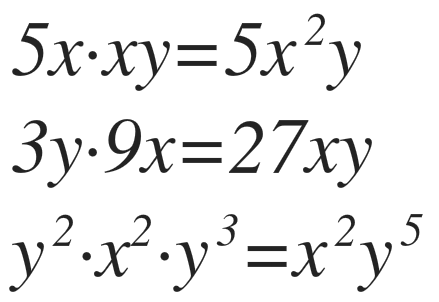
Ejercicios de monomios
1. Indica el grado de los siguientes monomios:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de monomios
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- ecuaciones 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) -3xy → grado = (2)
b) yz3 → grado = (4)
c) 8 → grado = (0)
d) 6n → grado = (1)
e)x5 / 8y → grado = (6)
Correcto
Incorrecto
-
2. Completa:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de monomios
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- ecuaciones 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) (m2+2m)-(5m2+8m)= (-4)m (2)- (6)m
b) xy33+7xy-xy+5xy3= (6)xy (3)+ (6)xy
c) 4a2+6b+a2-b= (5)a (2)+ (5)b
d) 3x2z-2xz2-(2x2z-xz2)+xz= (1)x (2)z+ (-1)xz (2)+ (1)xz
e) (a2bc+2abc2)-(c2ab+3ca2b)= (-2)a2bc+ (1)abc2
Correcto
Incorrecto
-
3. Completa:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de monomios
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- ecuaciones 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) (8x2)·(3xy)= (24)x (3)y (1)
b) (-ab)·(b-1)= (-1)a (1)
c) (m-3)·(mn)5=m (2)n (5)
d) (4xz)·(2x-1y)= (8)z (y)
e) (ac2)·(ab)=a (2) (b)c2
Correcto
Incorrecto
-

lo ame. tengo control en tres días, y no había prestado nada de atención a los zoom en clases virtuales, y esto me lo explico todo en unos minutos. realmente, 10/10