Los sistemas de ecuaciones están formados por 2 o más ecuaciones sobre las que queremos encontrar una solución común. Se llama solución de un sistema de ecuaciones a la solución común de las ecuaciones. Dicho de otro modo, la solución de un sistema de ecuaciones es el punto donde se cortan las rectas:
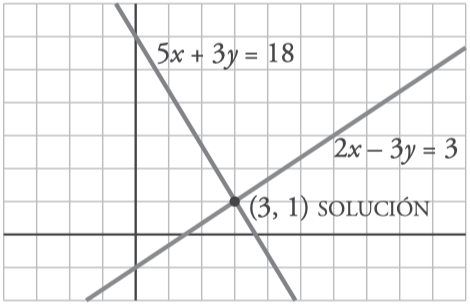
Los tres métodos para resolver un sistema de ecuaciones son:
– Método de sustitución
– Método de igualación
– Método de reducción.
Métodos de resolución de sistemas de ecuaciones
Método de sustitución
El método de sustitución consiste en despejar una de las incógnitas en cualquiera de las dos ecuaciones. Una vez aislada, el valor de dicha incógnita se sustituye en la otra ecuación. De esta forma, obtendremos otra ecuación, pero esta tendrá una sola incógnita. De esta forma, podemos resolver y sustituir con la solución de la incógnita en la otra ecuación.
Se trata de un proceso bastante sencillo y es muy útil cuando una de las incógnitas tiene coeficiente 1.
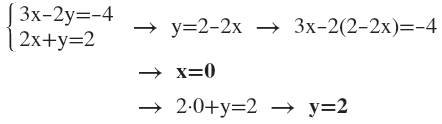
Método de igualación
Para realizar el método de igualación, lo primero que debemos hacer es despejar la misma incógnita en las dos ecuaciones. A continuación, se igualan los resultados. De esta manera, obtenemos una ecuación con una única incógnita. Se recomienda escoger este método cuando una misma incógnita es fácil de aislar en ambas ecuaciones.
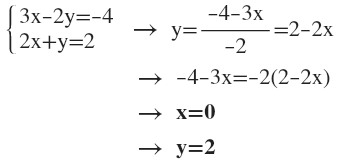
Método de reducción
EL método de reducción consiste en preparar las dos ecuaciones para que una de las incógnitas tenga el mismo coeficiente en ambas. Al restarlas o sumarlas se obtiene una ecuación sin esa incógnita. El uso de este método es muy útil cuando una misma incógnita tiene el mismo coeficiente en ambas ecuaciones. Si esto ocurre, restamos las ecuaciones, o las sumamos si tienen el mismo coeficiente y signo opuesto:
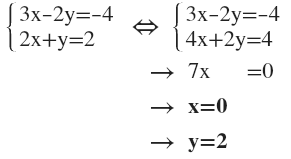
Ejercicios de sistemas de ecuaciones
1. Averigua las incógnitas aplicando el método de sustitución:
Ejercicios de sistemas de ecuaciones
2. Halla los valores de x e y aplicando el método de igualación:
Ejercicios de sistemas de ecuaciones
3. Aplica el método de reducción y resuelve el sistema:

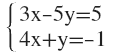
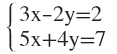
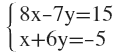
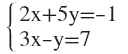
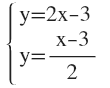
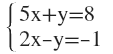
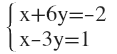
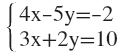
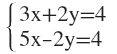
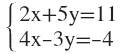
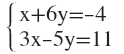
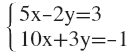
Muchas gracias… por ayudarme con mi tarea