Las ecuaciones de segundo grado son de la forma ax2+bx+c=0 siendo a distinto de cero. En función de los valores que tengan b y c estaremos hablando de ecuaciones completas o ecuaciones incompletas.
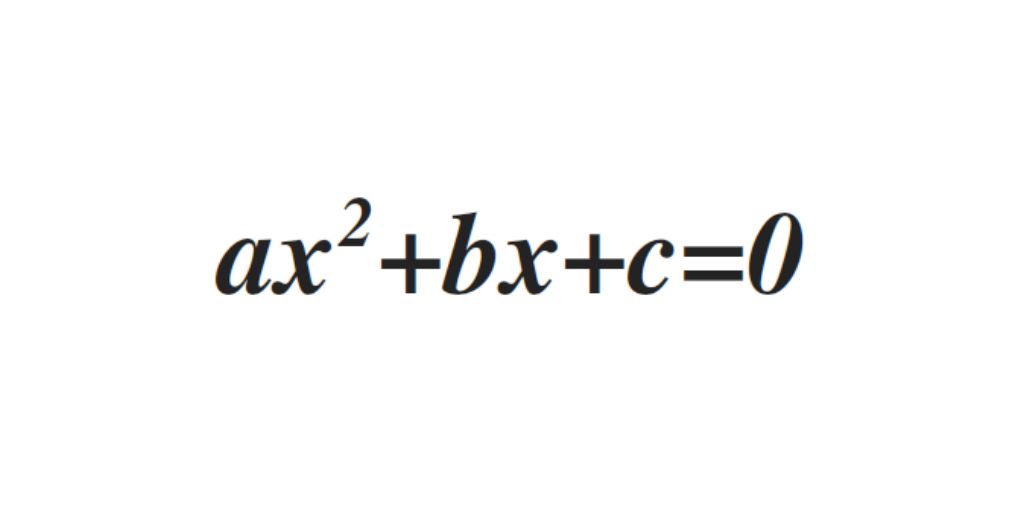
Ecuaciones de segundo grado completas
Las ecuaciones completas son aquellas que tienen b y c distintos de cero y se resuelve aplicando la siguiente fórmula:
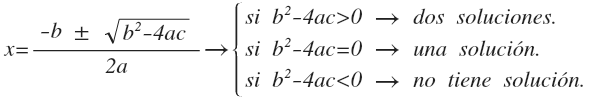
Ejemplo de ecuación de segundo grado completa:
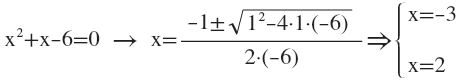
Discriminante de la ecuación
El discriminante de la ecuación sirve para saber el número de soluciones de una ecuación.

Ecuaciones incompletas
Las ecuaciones incompletas son aquellas en las que b=0 o c=0 y se pueden resolver con mucha sencillez, sin necesidad de aplicar ninguna fórmula.
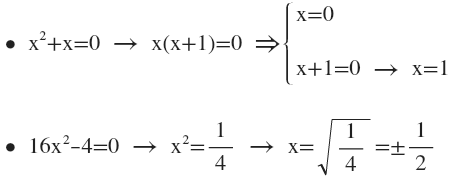
Ecuaciones factorizadas
Las ecuaciones factorizadas son las que tienen productos de factores en forma de paréntesis en los que aparecen una incógnita. Para su solución se eliminan los factores y se resuelve con la fórmula de las ecuaciones completas.
Ejemplo de ecuación factorizada:
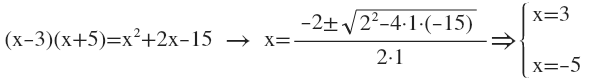
Para resolver una ecuación de este tipo:
Recuerda: para resolver ecuaciones de este tipo, es decir, “producto de varios factores igualado a cero”, igualamos a cero cada uno de los factores y resolvemos las correspondientes ecuaciones.
Ecuaciones con radicales
Las ecuaciones con radicales son aquellas que contienen raíces. como por ejemplo:
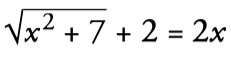
Como resolver ecuaciones con radicales
- Aislamos el radical en un miembro, pasando al otro lo demás:
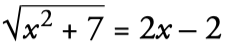
- Elevamos al cuadrado los dos miembros:

- Pasamos todo a un miembro y lo ordenamos:
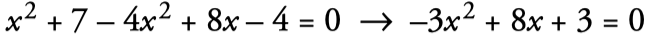
- Resolvemos la ecuación obtenida: (a=–3, b=8, c=3)
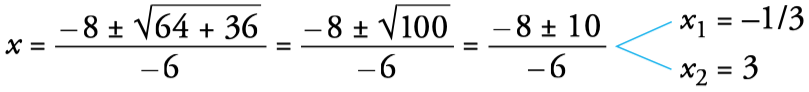
- En este tipo de ecuaciones con radicales, al elevar al cuadrado (2.° paso), pueden aparecer soluciones falsas. Por eso, es necesario comprobar las soluciones obtenidas sustituyéndolas en la ecuación inicial. En este caso, x=–1/3 no es solución, pero x=3 sí lo es. La ecuación tiene una solución: x=3
Ejercicios de ecuaciones de segundo grado
1. Calcula los valores de la incógnita e indícalos de menor a mayor:
Ejercicios de ecuaciones de segundo grado
2. Calcula e indica de menor a mayor los posibles soluciones:

0 comentarios