The quadratic equation is of the form ax2+bx+c=0 where a is nonzero. Depending on the values that b and c have, we will be talking about complete equations or incomplete equations.
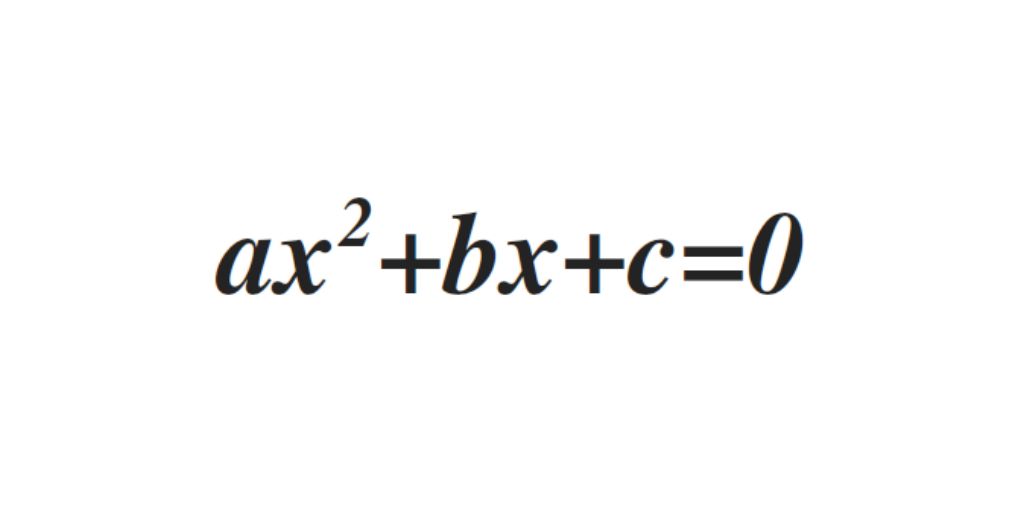
Complete quadratic equation
Complete quadratic equations are specific that have b and c other than zero and is solved by applying the following formula:
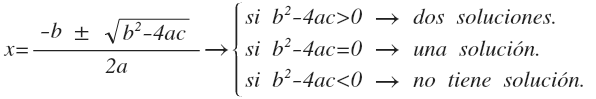
Example of a complete quadratic equation:
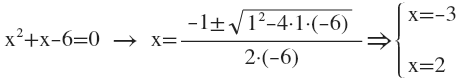
Discriminant equation
The discriminant of the equation is used to know the number of solutions of an equation.

Incomplete quadratic equation
The incomplete quadratic equation is that in which b=0 or c=0 and can be solved very simply, without the need to apply any formula.
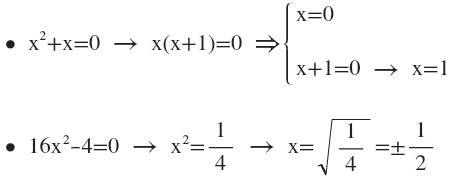
Factoring quadratics
The factoring quadratics are those that have factor products in the form of paralysis in which an unknown variable appears. For its solution the factors are eliminated and it is solved with the formula of the complete equations.
Example of factoring quadratic:
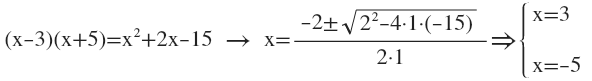
Remember: to solve quadratic equations, that is, “product of several factors equaled to zero”, we equal each factor to zero and solve the corresponding equations.
Radical equations
Radical equations are those that contain roots. for example:
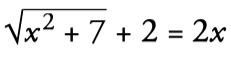
How to solve radicals equations:
- We isolate the radical in one member, passing the other to the other:
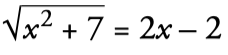
- We square the two members:

- We pass everything to a member and order it:
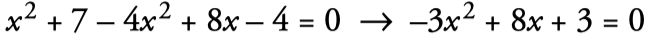
- We solve the obtained equation: (a=–3, b=8, c=3)
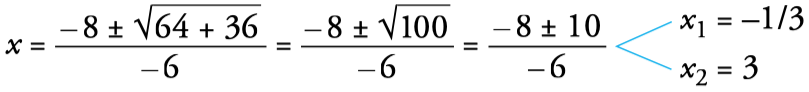
- In this type of radical equation, when squaring (2nd step), false solutions can appear. Therefore, it is necessary to check the solutions obtained by substituting them in the initial equation. In this case, x=–1/3 is not a solution, but x=3 is. The equation has a solution: x=3
Quadratic Equation Exercises
1. Calculate the values of the unknown and indicators from least to greatest:
Ejercicios de ecuaciones de segundo grado
2. Calculate and indicate the smallest possible solutions:

0 Comments