Linear equations are expressions that can reduce to the form ax+b=0, with a≠0. Their only solution is x=-(b/a) and the unknown x only appears raised to 1.
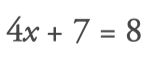
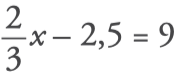
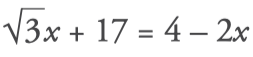
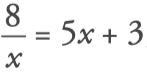
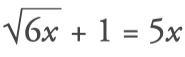
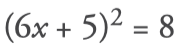
Equivalent equations
Two equations are equivalent if they have the same solution or both have no solution. Thus, the equations 5x–9=51 and 3x-7=89–5x are equivalent because the solution of both is x=12.
To solve an equation, we have to clear the x using a series of steps. Each step consists of transforming the equation into another equivalent equation, in which the x is closest to being cleared.
How to solve linear equations
Keep in mind the following rules to avoid making mistakes:
- Add or subtract the same expression in the two members of the equality. That is, what is adding in one member passes by subtracting the other member, and vice versa.
- Multiply or divide the two members by the same non-zero number. In other words, what is multiplying everything else from one member happens dividing the other, and vice versa.
How to solve a linear equation:
- Remove denominators, if any.
For this, the two members of the equation are multiplied by a common multiple of the denominators; preferably, their least common multiple:

- Remove parentheses, if any.
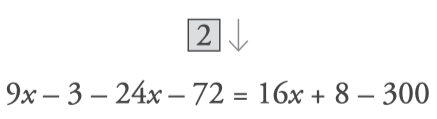
- Pass the x terms to one member and the numbers to the other member:
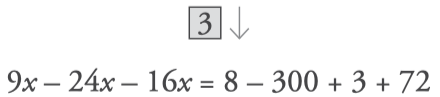
- Simplify each member:
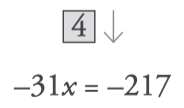
- Clear the x and get the solution like this:
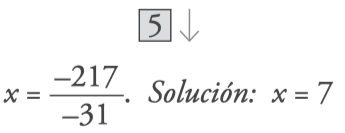
- Check by substituting the x for the solution obtained.
Since they match, the solution is correct:
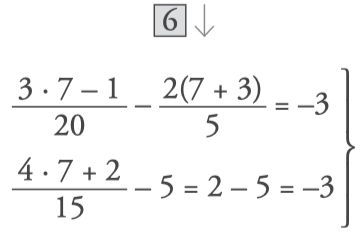
The best way to learn to solve linear equations is to practice doing lots of exercises. Start now and test yourself!
Linear equation exercises
1. Find out the value of x:
Ejercicios de ecuaciones
2. Solve the following equations:

0 Comments