An equation is an algebraic equality that have a relationship between quantities whose values are unknown and serve to solve problems. However, not all algebraic equalities are equations. An equation expresses, by means of algebraic equality, a relationship between quantities whose value, for the moment, we do not know.
What is an equation?
The equations are used to code relations in algebraic language and, from there, manage them mathematically. This is a very powerful tool for solving problems.
How to solve equations
Solving an equation is finding the value, or values, that the letters must take for equality to be true, or finding out that there is no solution. Surely, you know procedures to methodically solve some types of equations. But if we reach the solution by any other way, the resolution is also valid. The solution to the equation is the value of the unknown that makes equality true.
Examples of equation
A number → x
Its half → x / 2
His fifth part → x / 5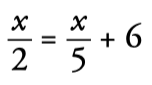
Laura’s age → x
Age within 28 years → x +28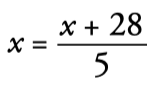
Width → x
Length → x + 3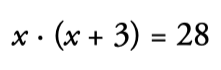
Elements of an equation
Members
They are each of the expressions that appear on both sides of the equality.
Terms
They are the addends that form the members.
Unknowns
They are the letters that appear in the equation.
Solutions
They are the values that the letters must take for equality to be fulfilled.
Grade
It is the highest of the degrees of the monomials that form the members.
Equivalent equations
Two equations are equivalent when they have the same unknowns and the same solutions.
Equations and identities
- An equation is an equality between algebraic expressions that holds only for certain letter values.
- An identity is an algebraic equality that is always fulfilled, regardless of the values that the letters take.
Solving equations
Type x+a=b
How to solve equations type x+a=b:
- To solve the equation x+a=b, we subtract a from both members.

- To solve the equation x+4=7:
We subtract 4 from the two members.
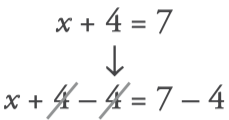
- The solution is x=3:
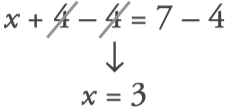
Type x-a=b
How to solve equations type x-a=b:
- To solve the equation x-a=b, we subtract a from both members.

- To solve x-2=6:
We add 2 to the two members: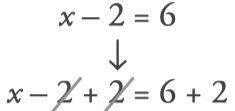
- The solution is x=8
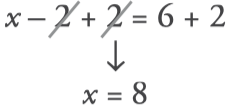
Exercises
1. Calculate the unknown in your mind:
Ejercicios de ecuaciones de primer grado
2. Apply what you have learned:

0 Comments