Los radicales son la raíz n-ésima de un número a:
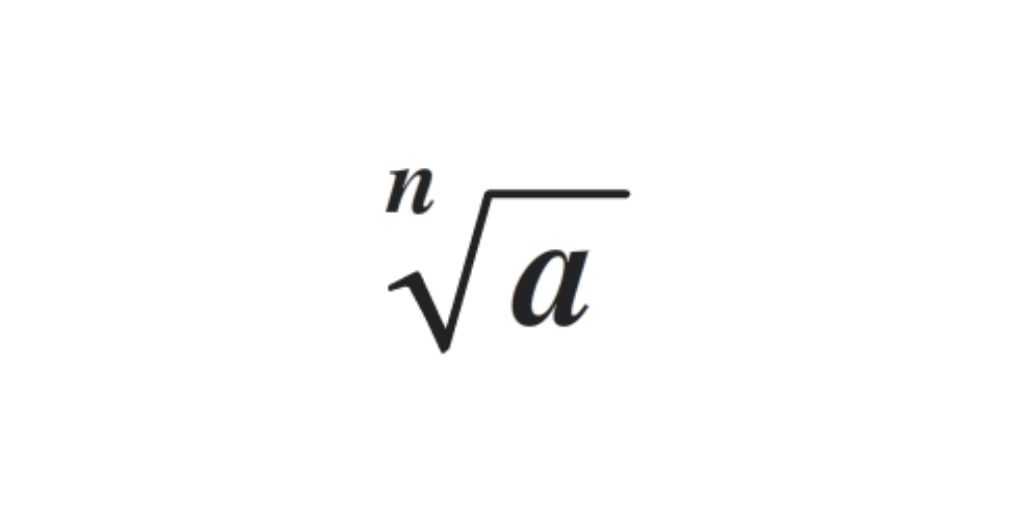
Siendo n el índice y a el radicando.
Propiedades
Radicales y potencias
Se puede expresar un radical en forma de potencia de la siguiente forma:
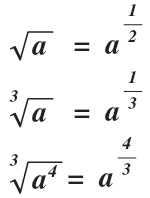
Simplificación
Para simplificar resulta más fácil expresar primero en forma de potencias.
Por tanto:

Extracción de factores
Para extraer factores de un radical hay que encontrar potencias dentro del radicando que tengan exponente mayor o igual que el índice del radical.
Por ejemplo:
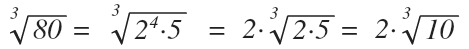
Potencia de un radical
Por ejemplo:
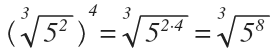
Raíces y radicales
La raíz de una raíz viene a ser otra raíz con el índice igual al producto de los índices de las dos raíces. Por ejemplo:

Ejercicios
1. Expresa en forma de potencia:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de radicales
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- números enteros 0%
- números reales 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) √4 = 4 (1)/ (2)
b) √73 = 7 (3)⁄ (2)
c) 3√5 = 5 (1)⁄ (3)
d) 3√95 = 9 (5)⁄ (3)
e) 6√811 = 8 (11)⁄ (6)
f) √125 = 12 (5)⁄ (2)
Correcto
Incorrecto
-
2. Simplifica:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de radicales
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- números reales 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) 6√23 = √2 (1)
b) 8√76 = (4)√7 (3)
c) 10√102 = (5)√10 (1)
d) 9√143 = (3)√14 (1)
e) 18√33 = (6)√3 (1)
f) 14√64 = (7)√6 (2)
Correcto
Incorrecto
-
3. Extrae los factores y expresa en forma de radical:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de radicales
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- números reales 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) 3√81 = 3√3 (4) = (3) · 3√ (3)
b) 6√128 = 6√2 (7) = (2) · 6√ (2)
c) √4000 = √2 (2) · 10 (3) = (20) · √ (10)
d) 5√10240 = √4 (5) · 10 (1) = (4) · 5√ (10)
e) 3√324 = 3√3 (4) · 4 (1) = (3) · 3√ (12)
Correcto
Incorrecto
-
4. Opera las potencias:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de radicales
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- números reales 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) (√23)5 = √2 (15)
b) (12√63)3 = 12√6 (9) = (4)√63
c) (48√638)2 = 48√63 (16) = (3)√63
d) (10√52)9 = 10√5 (18) = (5)√59
e) (33√83)10 = 33√8 (30) = 11√8 (10)
Correcto
Incorrecto
-
5. Simplifica las raíces:
SUmario del cuestionario
0 de 1 preguntas completado
Preguntas:
- 1
Información
Ejercicios de radicales
Ya has realizado este cuestionario antes. Por tanto, no puedes empezarlo otra vez.
Cargando el cuestionario...
Debes ser un usuario registrado para poder realizar el cuestionario.
Tienes que terminar antes el siguiente cuestionario, para iniciar este cuestionario:
Resultados
Tu tiempo:
El tiempo se ha terminado
Has conseguido 0 de 0 puntos posibles (0)
| Puntuación de promedio: |
|
| Tu puntuación |
|
Categorías
- números reales 0%
- 1
- Contestada
- Revisada
-
Pregunta 1 de 1
1. Pregunta
-
a) √√7 = (4)√7
b) 6√√3 = (12)√3
c) √ 5√4 · 5√8 = √5√ (32) = √ (2)
d) 9√ 8√ 144 = (72)√ 144 = (72)√ 12 (2) = (36)√ 12
e) 8√ 8√ 3 · 40√ 65 · 56√ 27 =
= 8√ 8√ (36) = (64)√ (36) = 64√ (6)2 = (36)√ 6
Correcto
Incorrecto
-

Pienso que la explicación deber ser más explícita y con muchos más ejemplos gracias.